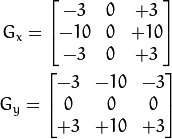Sobel 导数¶
原理¶
Note
以下内容来自于Bradski和Kaehler的大作: Learning OpenCV .
上面两节我们已经学习了卷积操作。一个最重要的卷积运算就是导数的计算(或者近似计算).
为什么对图像进行求导是重要的呢? 假设我们需要检测图像中的 边缘 ,如下图:

你可以看到在 边缘 ,相素值显著的 改变 了。表示这一 改变 的一个方法是使用 导数 。 梯度值的大变预示着图像中内容的显著变化。
用更加形象的图像来解释,假设我们有一张一维图形。下图中灰度值的”跃升”表示边缘的存在:
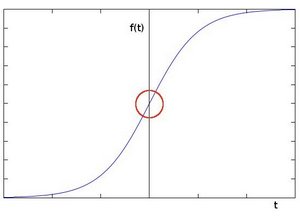
使用一阶微分求导我们可以更加清晰的看到边缘”跃升”的存在(这里显示为高峰值)
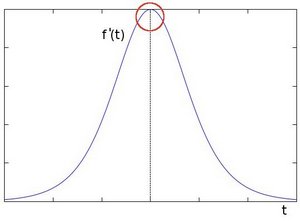
从上例中我们可以推论检测边缘可以通过定位梯度值大于邻域的相素的方法找到(或者推广到大于一个阀值).
更加详细的解释,请参考Bradski 和 Kaehler的 Learning OpenCV 。
源码¶
- 本程序做什么?
- 使用 Sobel算子 产生的输出图像上,检测到的亮起的 边缘 相素散布在更暗的背景中。
- 下面是本教程的源码,你也可以从 here 下载
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <stdlib.h>
#include <stdio.h>
using namespace cv;
/** @function main */
int main( int argc, char** argv )
{
Mat src, src_gray;
Mat grad;
char* window_name = "Sobel Demo - Simple Edge Detector";
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
int c;
/// 装载图像
src = imread( argv[1] );
if( !src.data )
{ return -1; }
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
/// 转换为灰度图
cvtColor( src, src_gray, CV_RGB2GRAY );
/// 创建显示窗口
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
/// 创建 grad_x 和 grad_y 矩阵
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
/// 求 X方向梯度
//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
/// 求Y方向梯度
//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );
/// 合并梯度(近似)
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
imshow( window_name, grad );
waitKey(0);
return 0;
}
解释¶
首先申明变量:
Mat src, src_gray; Mat grad; char* window_name = "Sobel Demo - Simple Edge Detector"; int scale = 1; int delta = 0; int ddepth = CV_16S;
装载原图像 src:
src = imread( argv[1] ); if( !src.data ) { return -1; }
第一步对原图像使用 GaussianBlur 降噪 ( 内核大小 = 3 )
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
将降噪后的图像转换为灰度图:
cvtColor( src, src_gray, CV_RGB2GRAY );
第二步,在 x 和 y 方向分别”求导“。 为此,我们使用函数 Sobel :
Mat grad_x, grad_y; Mat abs_grad_x, abs_grad_y; /// 求 X方向梯度 Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT ); /// 求 Y方向梯度 Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
该函数接受了以下参数:
- src_gray: 在本例中为输入图像,元素类型 CV_8U
- grad_x/grad_y: 输出图像.
- ddepth: 输出图像的深度,设定为 CV_16S 避免外溢。
- x_order: x 方向求导的阶数。
- y_order: y 方向求导的阶数。
- scale, delta 和 BORDER_DEFAULT: 使用默认值
注意为了在 x 方向求导我们使用:
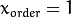 ,
, 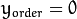 . 采用同样方法在 y 方向求导。
. 采用同样方法在 y 方向求导。将中间结果转换到 CV_8U:
convertScaleAbs( grad_x, abs_grad_x ); convertScaleAbs( grad_y, abs_grad_y );
将两个方向的梯度相加来求取近似 梯度 (注意这里没有准确的计算,但是对我们来讲已经足够了)。
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
最后,显示结果:
imshow( window_name, grad );
结果¶
这里是将Sobel算子作用于 lena.jpg 的结果:

翻译者¶
niesu@ OpenCV中文网站 <sisongasg@hotmail.com>
Help and Feedback
You did not find what you were looking for?- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.
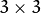 核的导数。
核的导数。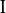 :
: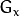 进行卷积。比如,当内核大小为3时,
进行卷积。比如,当内核大小为3时, 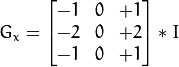
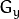 进行卷积。比如,当内核大小为3时,
进行卷积。比如,当内核大小为3时, 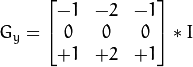
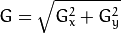
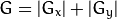
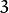 时, 以上Sobel内核可能产生比较明显的误差(毕竟,Sobel算子只是求取了导数的近似值)。 为解决这一问题,OpenCV提供了
时, 以上Sobel内核可能产生比较明显的误差(毕竟,Sobel算子只是求取了导数的近似值)。 为解决这一问题,OpenCV提供了