Navigation

图像平滑处理

目标

本教程教您怎样使用各种线性滤波器对图像进行平滑处理，相关OpenCV函数如下:

原理

Note

以下原理来源于Richard Szeliski 的著作 Computer Vision: Algorithms and Applications 以及 Learning OpenCV

  • 平滑 也称 模糊, 是一项简单且使用频率很高的图像处理方法。

  • 平滑处理的用途有很多， 但是在本教程中我们仅仅关注它减少噪声的功用 (其他用途在以后的教程中会接触到)。

  • 平滑处理时需要用到一个 滤波器 。 最常用的滤波器是 线性 滤波器，线性滤波处理的输出像素值 (i.e. 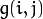g(i,j)) 是输入像素值 (i.e. 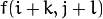f(i+k,j+l))的加权和 :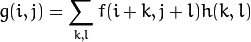

    g(i,j) = \sum_{k,l} f(i+k, j+l) h(k,l)

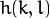    h(k,l) 称为 核, 它仅仅是一个加权系数。

    不妨把 滤波器 想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口滑过图像。

  • 滤波器的种类有很多， 这里仅仅提及最常用的:

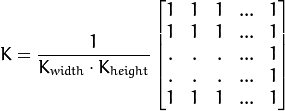
归一化块滤波器 (Normalized Box Filter)

  • 最简单的滤波器， 输出像素值是核窗口内像素值的 均值 ( 所有像素加权系数相等)

  • 核如下:

    K = \dfrac{1}{K_{width} \cdot K_{height}} \begin{bmatrix} 1 & 1 & 1 & ... & 1 \\ 1 & 1 & 1 & ... & 1 \\ . & . & . & ... & 1 \\ . & . & . & ... & 1 \\ 1 & 1 & 1 & ... & 1 \end{bmatrix}

高斯滤波器 (Gaussian Filter)

  • 最有用的滤波器 (尽管不是最快的)。 高斯滤波是将输入数组的每一个像素点与 高斯内核 卷积将卷积和当作输出像素值。

  • 还记得1维高斯函数的样子吗?

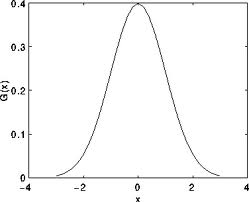
    ../../../../_images/Smoothing_Tutorial_theory_gaussian_0.jpg

    假设图像是1维的,那么观察上图，不难发现中间像素的加权系数是最大的， 周边像素的加权系数随着它们远离中间像素的距离增大而逐渐减小。

Note

2维高斯函数可以表达为 :

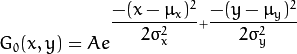
G_{0}(x, y) = A e^{ \dfrac{ -(x - \mu_{x})^{2} }{ 2\sigma^{2}_{x} } + \dfrac{ -(y - \mu_{y})^{2} }{ 2\sigma^{2}_{y} } }

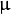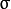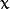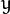其中 \mu 为均值 (峰值对应位置)， \sigma 代表标准差 (变量 x 和 变量 y 各有一个均值，也各有一个标准差)

中值滤波器 (Median Filter)

中值滤波将图像的每个像素用邻域 (以当前像素为中心的正方形区域)像素的 中值 代替 。

双边滤波 (Bilateral Filter)

  • 目前我们了解的滤波器都是为了 平滑 图像， 问题是有些时候这些滤波器不仅仅削弱了噪声， 连带着把边缘也给磨掉了。 为避免这样的情形 (至少在一定程度上 ), 我们可以使用双边滤波。
  • 类似于高斯滤波器，双边滤波器也给每一个邻域像素分配一个加权系数。 这些加权系数包含两个部分, 第一部分加权方式与高斯滤波一样，第二部分的权重则取决于该邻域像素与当前像素的灰度差值。
  • 详细的解释可以查看 链接

源码

  • 本程序做什么?

    • 装载一张图像
    • 使用4种不同滤波器 (见原理部分) 并显示平滑图像

  • 下载代码: 点击 这里

  • 代码一瞥:

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"

using namespace std;
using namespace cv;

/// 全局变量
int DELAY_CAPTION = 1500;
int DELAY_BLUR = 100;
int MAX_KERNEL_LENGTH = 31;

Mat src; Mat dst;
char window_name[] = "Filter Demo 1";

/// 函数申明
int display_caption( char* caption );
int display_dst( int delay );

/**
 *  main 函数
 */
 int main( int argc, char** argv )
 {
   namedWindow( window_name, CV_WINDOW_AUTOSIZE );

   /// 载入原图像
   src = imread( "../images/lena.jpg", 1 );

   if( display_caption( "Original Image" ) != 0 ) { return 0; }

   dst = src.clone();
   if( display_dst( DELAY_CAPTION ) != 0 ) { return 0; }

   /// 使用 均值平滑
   if( display_caption( "Homogeneous Blur" ) != 0 ) { return 0; }

   for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
       { blur( src, dst, Size( i, i ), Point(-1,-1) );
         if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

    /// 使用高斯平滑
    if( display_caption( "Gaussian Blur" ) != 0 ) { return 0; }

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
        { GaussianBlur( src, dst, Size( i, i ), 0, 0 );
          if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

     /// 使用中值平滑
     if( display_caption( "Median Blur" ) != 0 ) { return 0; }

     for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
         { medianBlur ( src, dst, i );
           if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

     /// 使用双边平滑
     if( display_caption( "Bilateral Blur" ) != 0 ) { return 0; }

     for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
         { bilateralFilter ( src, dst, i, i*2, i/2 );
           if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

     /// 等待用户输入
     display_caption( "End: Press a key!" );

     waitKey(0);
     return 0;
 }

 int display_caption( char* caption )
 {
   dst = Mat::zeros( src.size(), src.type() );
   putText( dst, caption,
            Point( src.cols/4, src.rows/2),
            CV_FONT_HERSHEY_COMPLEX, 1, Scalar(255, 255, 255) );

   imshow( window_name, dst );
   int c = waitKey( DELAY_CAPTION );
   if( c >= 0 ) { return -1; }
   return 0;
  }

  int display_dst( int delay )
  {
    imshow( window_name, dst );
    int c = waitKey ( delay );
    if( c >= 0 ) { return -1; }
    return 0;
  }

解释

  1. 下面看一看有关平滑的OpenCV函数，其余部分大家已经很熟了。

  2. 归一化块滤波器:

    OpenCV函数 blur 执行了归一化块平滑操作。

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    { blur( src, dst, Size( i, i ), Point(-1,-1) );
      if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

    我们输入4个实参 (详细的解释请参考 Reference):

    • src: 输入图像
    • dst: 输出图像
    • Size( w,h ): 定义内核大小( w 像素宽度， h 像素高度)
    • Point(-1, -1): 指定锚点位置(被平滑点)， 如果是负值，取核的中心为锚点。

  3. 高斯滤波器:

    OpenCV函数 GaussianBlur 执行高斯平滑 :

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    { GaussianBlur( src, dst, Size( i, i ), 0, 0 );
      if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

我们输入4个实参 (详细的解释请参考 Reference):

  • src: 输入图像
  • dst: 输出图像
  • Size(w, h): 定义内核的大小(需要考虑的邻域范围)。 w 和 h 必须是正奇数，否则将使用 \sigma_{x} 和 \sigma_{y} 参数来计算内核大小。
  • \sigma_{x}: x 方向标准方差， 如果是 0 则 \sigma_{x} 使用内核大小计算得到。
  • \sigma_{y}: y 方向标准方差， 如果是 0 则 \sigma_{y} 使用内核大小计算得到。.

  1. 中值滤波器:

    OpenCV函数 medianBlur 执行中值滤波操作:

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    { medianBlur ( src, dst, i );
      if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

    我们用了3个参数:

    • src: 输入图像
    • dst: 输出图像, 必须与 src 相同类型
    • i: 内核大小 (只需一个值，因为我们使用正方形窗口)，必须为奇数。

  2. 双边滤波器

    OpenCV函数 bilateralFilter 执行双边滤波操作:

    for ( int i = 1; i < MAX_KERNEL_LENGTH; i = i + 2 )
    { bilateralFilter ( src, dst, i, i*2, i/2 );
      if( display_dst( DELAY_BLUR ) != 0 ) { return 0; } }

    我们使用了5个参数:

    • src: 输入图像
    • dst: 输出图像
    • d: 像素的邻域直径
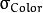    • \sigma_{Color}: 颜色空间的标准方差
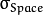    • \sigma_{Space}: 坐标空间的标准方差(像素单位)

结果

  • 程序显示了原始图像( lena.jpg) 和使用4种滤波器之后的效果图。

  • 这里显示的是使用 中值滤波 之后的效果图:

    Smoothing with a median filter

Table Of Contents

Previous topic

imgproc 模块. 图像处理

Next topic

腐蚀与膨胀(Eroding and Dilating)

This Page

Navigation

© Copyright 2011, opencv dev team. Last updated on Mar 30, 2012. Created using Sphinx 1.1.3.