Expectation Maximization¶
The Expectation Maximization(EM) algorithm estimates the parameters of the multivariate probability density function in the form of a Gaussian mixture distribution with a specified number of mixtures.
Consider the set of the N feature vectors
{ 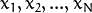 } from a d-dimensional Euclidean space drawn from a Gaussian mixture:
} from a d-dimensional Euclidean space drawn from a Gaussian mixture:
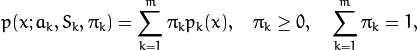
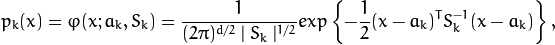
where
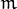 is the number of mixtures,
is the number of mixtures,
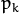 is the normal distribution
density with the mean
is the normal distribution
density with the mean
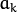 and covariance matrix
and covariance matrix
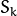 ,
,
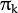 is the weight of the k-th mixture. Given the number of mixtures
is the weight of the k-th mixture. Given the number of mixtures
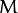 and the samples
and the samples
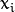 ,
,
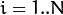 the algorithm finds the
maximum-likelihood estimates (MLE) of all the mixture parameters,
that is,
the algorithm finds the
maximum-likelihood estimates (MLE) of all the mixture parameters,
that is,
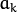 ,
,
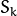 and
and
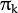 :
:
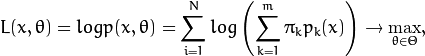
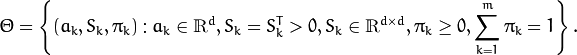
The EM algorithm is an iterative procedure. Each iteration includes
two steps. At the first step (Expectation step or E-step), you find a
probability
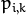 (denoted
(denoted
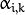 in the formula below) of
sample i to belong to mixture k using the currently
available mixture parameter estimates:
in the formula below) of
sample i to belong to mixture k using the currently
available mixture parameter estimates:
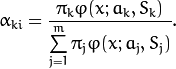
At the second step (Maximization step or M-step), the mixture parameter estimates are refined using the computed probabilities:
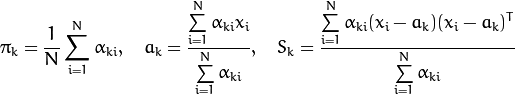
Alternatively, the algorithm may start with the M-step when the initial values for
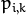 can be provided. Another alternative when
can be provided. Another alternative when
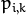 are unknown is to use a simpler clustering algorithm to pre-cluster the input samples and thus obtain initial
are unknown is to use a simpler clustering algorithm to pre-cluster the input samples and thus obtain initial
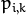 . Often (including macnine learning) the
kmeans() algorithm is used for that purpose.
. Often (including macnine learning) the
kmeans() algorithm is used for that purpose.
One of the main problems of the EM algorithm is a large number
of parameters to estimate. The majority of the parameters reside in
covariance matrices, which are
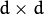 elements each
where
elements each
where
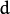 is the feature space dimensionality. However, in
many practical problems, the covariance matrices are close to diagonal
or even to
is the feature space dimensionality. However, in
many practical problems, the covariance matrices are close to diagonal
or even to
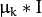 , where
, where
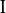 is an identity matrix and
is an identity matrix and
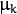 is a mixture-dependent “scale” parameter. So, a robust computation
scheme could start with harder constraints on the covariance
matrices and then use the estimated parameters as an input for a less
constrained optimization problem (often a diagonal covariance matrix is
already a good enough approximation).
is a mixture-dependent “scale” parameter. So, a robust computation
scheme could start with harder constraints on the covariance
matrices and then use the estimated parameters as an input for a less
constrained optimization problem (often a diagonal covariance matrix is
already a good enough approximation).
References:
- Bilmes98 J. A. Bilmes. A Gentle Tutorial of the EM Algorithm and its Application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models. Technical Report TR-97-021, International Computer Science Institute and Computer Science Division, University of California at Berkeley, April 1998.
CvEMParams¶
- class CvEMParams¶
Parameters of the EM algorithm. All parameters are public. You can initialize them by a constructor and then override some of them directly if you want.
CvEMParams::CvEMParams¶
The constructors
- C++: CvEMParams::CvEMParams()¶
- C++: CvEMParams::CvEMParams(int nclusters, int cov_mat_type=CvEM::COV_MAT_DIAGONAL, int start_step=CvEM::START_AUTO_STEP, CvTermCriteria term_crit=cvTermCriteria(CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 100, FLT_EPSILON), const CvMat* probs=0, const CvMat* weights=0, const CvMat* means=0, const CvMat** covs=0 )¶
Parameters: - nclusters – The number of mixture components in the gaussian mixture model. Some of EM implementation could determine the optimal number of mixtures within a specified value range, but that is not the case in ML yet.
- cov_mat_type –
Constraint on covariance matrices which defines type of matrices. Possible values are:
- CvEM::COV_MAT_SPHERICAL A scaled identity matrix
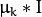 . There is the only parameter
. There is the only parameter 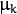 to be estimated for earch matrix. The option may be used in special cases, when the constraint is relevant, or as a first step in the optimization (for example in case when the data is preprocessed with PCA). The results of such preliminary estimation may be passed again to the optimization procedure, this time with cov_mat_type=CvEM::COV_MAT_DIAGONAL.
to be estimated for earch matrix. The option may be used in special cases, when the constraint is relevant, or as a first step in the optimization (for example in case when the data is preprocessed with PCA). The results of such preliminary estimation may be passed again to the optimization procedure, this time with cov_mat_type=CvEM::COV_MAT_DIAGONAL. - CvEM::COV_MAT_DIAGONAL A diagonal matrix with positive diagonal elements. The number of free parameters is d for each matrix. This is most commonly used option yielding good estimation results.
- CvEM::COV_MAT_GENERIC A symmetric positively defined matrix. The number of free parameters in each matrix is about
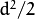 . It is not recommended to use this option, unless there is pretty accurate initial estimation of the parameters and/or a huge number of training samples.
. It is not recommended to use this option, unless there is pretty accurate initial estimation of the parameters and/or a huge number of training samples.
- CvEM::COV_MAT_SPHERICAL A scaled identity matrix
- start_step –
The start step of the EM algorithm:
- CvEM::START_E_STEP Start with Expectation step. You need to provide means
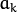 of mixture components to use this option. Optionally you can pass weights
of mixture components to use this option. Optionally you can pass weights 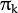 and covariance matrices
and covariance matrices 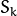 of mixture components.
of mixture components. - CvEM::START_M_STEP Start with Maximization step. You need to provide initial probabilites
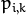 to use this option.
to use this option. - CvEM::START_AUTO_STEP Start with Expectation step. You need not provide any parameters because they will be estimated by the k-means algorithm.
- CvEM::START_E_STEP Start with Expectation step. You need to provide means
- term_crit – The termination criteria of the EM algorithm. The EM algorithm can be terminated by the number of iterations term_crit.max_iter (number of M-steps) or when relative change of likelihood logarithm is less than term_crit.epsilon.
- probs – Initial probabilities
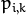 of sample
of sample  to belong to mixture component
to belong to mixture component 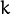 . It is a floating-point matrix of
. It is a floating-point matrix of 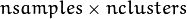 size. It is used and must be not NULL only when start_step=CvEM::START_M_STEP.
size. It is used and must be not NULL only when start_step=CvEM::START_M_STEP. - weights – Initial weights
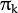 of mixture components. It is a floating-point vector with
of mixture components. It is a floating-point vector with 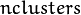 elements. It is used (if not NULL) only when start_step=CvEM::START_E_STEP.
elements. It is used (if not NULL) only when start_step=CvEM::START_E_STEP. - means – Initial means
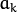 of mixture components. It is a floating-point matrix of
of mixture components. It is a floating-point matrix of 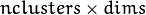 size. It is used used and must be not NULL only when start_step=CvEM::START_E_STEP.
size. It is used used and must be not NULL only when start_step=CvEM::START_E_STEP. - covs – Initial covariance matrices
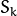 of mixture components. Each of covariance matrices is a valid square floating-point matrix of
of mixture components. Each of covariance matrices is a valid square floating-point matrix of 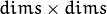 size. It is used (if not NULL) only when start_step=CvEM::START_E_STEP.
size. It is used (if not NULL) only when start_step=CvEM::START_E_STEP.
The default constructor represents a rough rule-of-the-thumb:
CvEMParams() : nclusters(10), cov_mat_type(1/*CvEM::COV_MAT_DIAGONAL*/),
start_step(0/*CvEM::START_AUTO_STEP*/), probs(0), weights(0), means(0), covs(0)
{
term_crit=cvTermCriteria( CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, 100, FLT_EPSILON );
}
With another contstructor it is possible to override a variety of parameters from a single number of mixtures (the only essential problem-dependent parameter) to initial values for the mixture parameters.
CvEM¶
- class CvEM¶
The class implements the EM algorithm as described in the beginning of this section.
CvEM::train¶
Estimates the Gaussian mixture parameters from a sample set.
- C++: void CvEM::train(const Mat& samples, const Mat& sample_idx=Mat(), CvEMParams params=CvEMParams(), Mat* labels=0 )¶
- C++: bool CvEM::train(const CvMat* samples, const CvMat* sampleIdx=0, CvEMParams params=CvEMParams(), CvMat* labels=0 )¶
- Python: cv2.EM.train(samples[, sampleIdx[, params]]) → retval, labels¶
Parameters: - samples – Samples from which the Gaussian mixture model will be estimated.
- sample_idx – Mask of samples to use. All samples are used by default.
- params – Parameters of the EM algorithm.
- labels – The optional output “class label” for each sample:
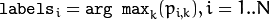 (indices of the most probable mixture component for each sample).
(indices of the most probable mixture component for each sample).
Unlike many of the ML models, EM is an unsupervised learning algorithm and it does not take responses (class labels or function values) as input. Instead, it computes the
Maximum Likelihood Estimate of the Gaussian mixture parameters from an input sample set, stores all the parameters inside the structure:
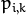 in probs,
in probs,
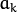 in means ,
in means ,
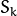 in covs[k],
in covs[k],
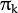 in weights , and optionally computes the output “class label” for each sample:
in weights , and optionally computes the output “class label” for each sample:
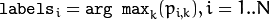 (indices of the most probable mixture component for each sample).
(indices of the most probable mixture component for each sample).
The trained model can be used further for prediction, just like any other classifier. The trained model is similar to the CvNormalBayesClassifier.
For an example of clustering random samples of the multi-Gaussian distribution using EM, see em.cpp sample in the OpenCV distribution.
CvEM::predict¶
Returns a mixture component index of a sample.
- C++: float CvEM::predict(const Mat& sample, Mat* probs=0 ) const¶
- C++: float CvEM::predict(const CvMat* sample, CvMat* probs) const¶
- Python: cv2.EM.predict(sample) → retval, probs¶
Parameters: - sample – A sample for classification.
- probs – If it is not null then the method will write posterior probabilities of each component given the sample data to this parameter.
CvEM::getNClusters¶
Returns the number of mixture components 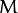 in the gaussian mixture model.
in the gaussian mixture model.
- C++: int CvEM::getNClusters() const¶
- C++: int CvEM::get_nclusters() const¶
- Python: cv2.EM.getNClusters() → retval¶
CvEM::getMeans¶
Returns mixture means 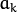 .
.
- C++: Mat CvEM::getMeans() const¶
- C++: const CvMat* CvEM::get_means() const¶
- Python: cv2.EM.getMeans() → means¶
CvEM::getCovs¶
Returns mixture covariance matrices 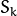 .
.
- C++: void CvEM::getCovs(std::vector<cv::Mat>& covs) const¶
- C++: const CvMat** CvEM::get_covs() const¶
- Python: cv2.EM.getCovs([covs]) → covs¶
CvEM::getWeights¶
Returns mixture weights 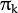 .
.
- C++: Mat CvEM::getWeights() const¶
- C++: const CvMat* CvEM::get_weights() const¶
- Python: cv2.EM.getWeights() → weights¶
CvEM::getProbs¶
Returns vectors of probabilities for each training sample.
- C++: Mat CvEM::getProbs() const¶
- C++: const CvMat* CvEM::get_probs() const¶
- Python: cv2.EM.getProbs() → probs¶
For each training sample  (that have been passed to the constructor or to CvEM::train()) returns probabilites
(that have been passed to the constructor or to CvEM::train()) returns probabilites 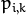 to belong to a mixture component
to belong to a mixture component 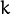 .
.
CvEM::getLikelihood¶
Returns logarithm of likelihood.
- C++: double CvEM::getLikelihood() const¶
- C++: double CvEM::get_log_likelihood() const¶
- Python: cv2.EM.getLikelihood() → likelihood¶
CvEM::getLikelihoodDelta¶
Returns difference between logarithm of likelihood on the last iteration and logarithm of likelihood on the previous iteration.
- C++: double CvEM::getLikelihoodDelta() const¶
- C++: double CvEM::get_log_likelihood_delta() const¶
- Python: cv2.EM.getLikelihoodDelta() → likelihood delta¶
CvEM::write_params¶
Writes used parameters of the EM algorithm to a file storage.
- C++: void CvEM::write_params(CvFileStorage* fs) const¶
Parameters: - fs – A file storage where parameters will be written.
CvEM::read_params¶
Reads parameters of the EM algorithm.
- C++: void CvEM::read_params(CvFileStorage* fs, CvFileNode* node)¶
Parameters: - fs – A file storage with parameters of the EM algorithm.
- node – The parent map. If it is NULL, the function searches a node with parameters in all the top-level nodes (streams), starting with the first one.
The function reads EM parameters from the specified file storage node. For example of clustering random samples of multi-Gaussian distribution using EM see em.cpp sample in OpenCV distribution.
Help and Feedback
You did not find what you were looking for?- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.