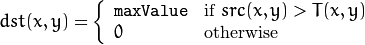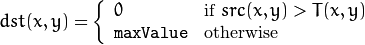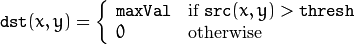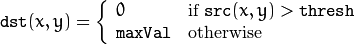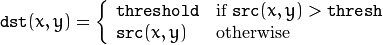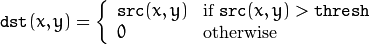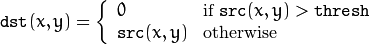Miscellaneous Image Transformations¶
adaptiveThreshold¶
Applies an adaptive threshold to an array.
- C++: void adaptiveThreshold(InputArray src, OutputArray dst, double maxValue, int adaptiveMethod, int thresholdType, int blockSize, double C)¶
- Python: cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C[, dst]) → dst¶
- C: void cvAdaptiveThreshold(const CvArr* src, CvArr* dst, double maxValue, int adaptiveMethod=CV_ADAPTIVE_THRESH_MEAN_C, int thresholdType=CV_THRESH_BINARY, int blockSize=3, double param1=5 )¶
- Python: cv.AdaptiveThreshold(src, dst, maxValue, adaptiveMethod=CV_ADAPTIVE_THRESH_MEAN_C, thresholdType=CV_THRESH_BINARY, blockSize=3, param1=5) → None¶
Parameters: - src – Source 8-bit single-channel image.
- dst – Destination image of the same size and the same type as src .
- maxValue – Non-zero value assigned to the pixels for which the condition is satisfied. See the details below.
- adaptiveMethod – Adaptive thresholding algorithm to use, ADAPTIVE_THRESH_MEAN_C or ADAPTIVE_THRESH_GAUSSIAN_C . See the details below.
- thresholdType – Thresholding type that must be either THRESH_BINARY or THRESH_BINARY_INV .
- blockSize – Size of a pixel neighborhood that is used to calculate a threshold value for the pixel: 3, 5, 7, and so on.
- C – Constant subtracted from the mean or weighted mean (see the details below). Normally, it is positive but may be zero or negative as well.
The function transforms a grayscale image to a binary image according to the formulae:
THRESH_BINARY
THRESH_BINARY_INV
where
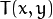 is a threshold calculated individually for each pixel.
is a threshold calculated individually for each pixel.
- For the method ADAPTIVE_THRESH_MEAN_C , the threshold value
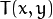 is a mean of the
is a mean of the
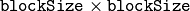 neighborhood of
neighborhood of
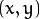 minus C .
minus C . - For the method ADAPTIVE_THRESH_GAUSSIAN_C , the threshold value
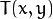 is a weighted sum (cross-correlation with a Gaussian window) of the
is a weighted sum (cross-correlation with a Gaussian window) of the
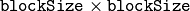 neighborhood of
neighborhood of
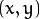 minus C . The default sigma (standard deviation) is used for the specified blockSize . See
getGaussianKernel() .
minus C . The default sigma (standard deviation) is used for the specified blockSize . See
getGaussianKernel() .
The function can process the image in-place.
See also
threshold(), blur(), GaussianBlur()
cvtColor¶
Converts an image from one color space to another.
- C++: void cvtColor(InputArray src, OutputArray dst, int code, int dstCn=0 )¶
- Python: cv2.cvtColor(src, code[, dst[, dstCn]]) → dst¶
- C: void cvCvtColor(const CvArr* src, CvArr* dst, int code)¶
- Python: cv.CvtColor(src, dst, code) → None¶
Parameters: - src – Source image: 8-bit unsigned, 16-bit unsigned ( CV_16UC... ), or single-precision floating-point.
- dst – Destination image of the same size and depth as src .
- code – Color space conversion code. See the description below.
- dstCn – Number of channels in the destination image. If the parameter is 0, the number of the channels is derived automatically from src and code .
The function converts an input image from one color space to another. In case of a transformation to-from RGB color space, the order of the channels should be specified explicitly (RGB or BGR). Note that the default color format in OpenCV is often referred to as RGB but it is actually BGR (the bytes are reversed). So the first byte in a standard (24-bit) color image will be an 8-bit Blue component, the second byte will be Green, and the third byte will be Red. The fourth, fifth, and sixth bytes would then be the second pixel (Blue, then Green, then Red), and so on.
The conventional ranges for R, G, and B channel values are:
- 0 to 255 for CV_8U images
- 0 to 65535 for CV_16U images
- 0 to 1 for CV_32F images
In case of linear transformations, the range does not matter.
But in case of a non-linear transformation, an input RGB image should be normalized to the proper value range to get the correct results, for example, for RGB
 L*u*v* transformation. For example, if you have a 32-bit floating-point image directly converted from an 8-bit image without any scaling, then it will have the 0..255 value range instead of 0..1 assumed by the function. So, before calling cvtColor , you need first to scale the image down:
L*u*v* transformation. For example, if you have a 32-bit floating-point image directly converted from an 8-bit image without any scaling, then it will have the 0..255 value range instead of 0..1 assumed by the function. So, before calling cvtColor , you need first to scale the image down:
img *= 1./255;
cvtColor(img, img, CV_BGR2Luv);
If you use cvtColor with 8-bit images, the conversion will have some information lost. For many applications, this will not be noticeable but it is recommended to use 32-bit images in applications that need the full range of colors or that convert an image before an operation and then convert back.
The function can do the following transformations:
Transformations within RGB space like adding/removing the alpha channel, reversing the channel order, conversion to/from 16-bit RGB color (R5:G6:B5 or R5:G5:B5), as well as conversion to/from grayscale using:
![\text{RGB[A] to Gray:} \quad Y \leftarrow 0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot B](../../../_images/math/aec60f2c1832bb07ad040335189257e97afd00d6.png)
and
![\text{Gray to RGB[A]:} \quad R \leftarrow Y, G \leftarrow Y, B \leftarrow Y, A \leftarrow 0](../../../_images/math/8f5c51f3a4cae34d417208c8f561b2b5e264dc41.png)
The conversion from a RGB image to gray is done with:
cvtColor(src, bwsrc, CV_RGB2GRAY);
More advanced channel reordering can also be done with mixChannels() .
RGB
 CIE XYZ.Rec 709 with D65 white point ( CV_BGR2XYZ, CV_RGB2XYZ, CV_XYZ2BGR, CV_XYZ2RGB ):
CIE XYZ.Rec 709 with D65 white point ( CV_BGR2XYZ, CV_RGB2XYZ, CV_XYZ2BGR, CV_XYZ2RGB ):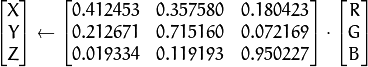
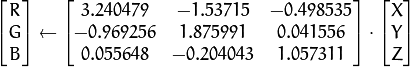
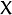 ,
, 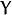 and
and
 cover the whole value range (in case of floating-point images,
cover the whole value range (in case of floating-point images,
 may exceed 1).
may exceed 1).RGB
 YCrCb JPEG (or YCC) ( CV_BGR2YCrCb, CV_RGB2YCrCb, CV_YCrCb2BGR, CV_YCrCb2RGB )
YCrCb JPEG (or YCC) ( CV_BGR2YCrCb, CV_RGB2YCrCb, CV_YCrCb2BGR, CV_YCrCb2RGB )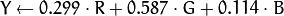
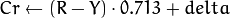
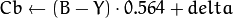
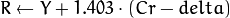
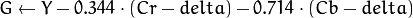
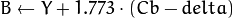
where
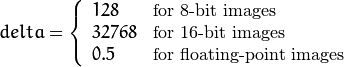
Y, Cr, and Cb cover the whole value range.
- RGB
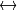 HSV ( CV_BGR2HSV, CV_RGB2HSV, CV_HSV2BGR, CV_HSV2RGB )
HSV ( CV_BGR2HSV, CV_RGB2HSV, CV_HSV2BGR, CV_HSV2RGB ) In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
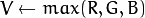
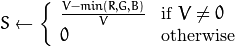
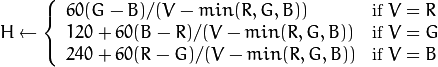
If
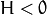 then
then
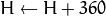 . On output
. On output
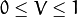 ,
, 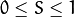 ,
, 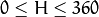 .
.The values are then converted to the destination data type:
8-bit images
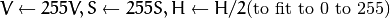
16-bit images (currently not supported)
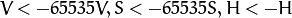
- 32-bit images
H, S, and V are left as is
- RGB
- RGB
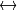 HLS ( CV_BGR2HLS, CV_RGB2HLS, CV_HLS2BGR, CV_HLS2RGB ).
HLS ( CV_BGR2HLS, CV_RGB2HLS, CV_HLS2BGR, CV_HLS2RGB ). In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
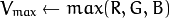
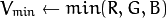
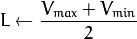
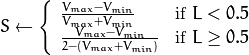
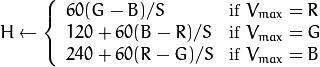
If
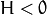 then
then
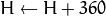 . On output
. On output
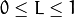 ,
, 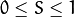 ,
, 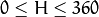 .
.The values are then converted to the destination data type:
8-bit images
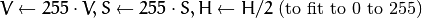
16-bit images (currently not supported)
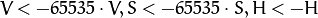
- 32-bit images
H, S, V are left as is
- RGB
- RGB
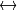 CIE L*a*b* ( CV_BGR2Lab, CV_RGB2Lab, CV_Lab2BGR, CV_Lab2RGB ).
CIE L*a*b* ( CV_BGR2Lab, CV_RGB2Lab, CV_Lab2BGR, CV_Lab2RGB ). In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit the 0 to 1 range.
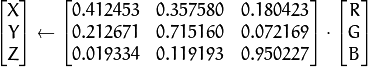
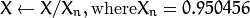
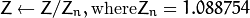
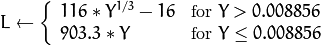
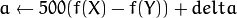
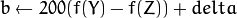
where
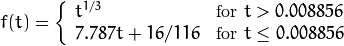
and
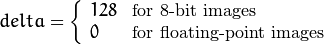
This outputs
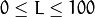 ,
, 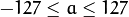 ,
, 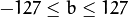 . The values are then converted to the destination data type:
. The values are then converted to the destination data type:8-bit images
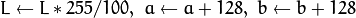
- 16-bit images
(currently not supported)
- 32-bit images
L, a, and b are left as is
- RGB
- RGB
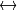 CIE L*u*v* ( CV_BGR2Luv, CV_RGB2Luv, CV_Luv2BGR, CV_Luv2RGB ).
CIE L*u*v* ( CV_BGR2Luv, CV_RGB2Luv, CV_Luv2BGR, CV_Luv2RGB ). In case of 8-bit and 16-bit images, R, G, and B are converted to the floating-point format and scaled to fit 0 to 1 range.
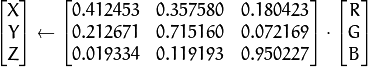
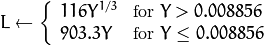
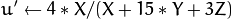
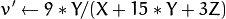
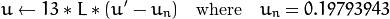
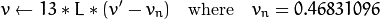
This outputs
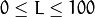 ,
, 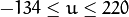 ,
, 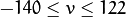 .
.The values are then converted to the destination data type:
8-bit images
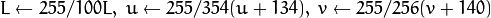
- 16-bit images
(currently not supported)
- 32-bit images
L, u, and v are left as is
The above formulae for converting RGB to/from various color spaces have been taken from multiple sources on the web, primarily from the Charles Poynton site http://www.poynton.com/ColorFAQ.html
- RGB
Bayer
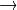 RGB ( CV_BayerBG2BGR, CV_BayerGB2BGR, CV_BayerRG2BGR, CV_BayerGR2BGR, CV_BayerBG2RGB, CV_BayerGB2RGB, CV_BayerRG2RGB, CV_BayerGR2RGB ). The Bayer pattern is widely used in CCD and CMOS cameras. It enables you to get color pictures from a single plane where R,G, and B pixels (sensors of a particular component) are interleaved as follows:
RGB ( CV_BayerBG2BGR, CV_BayerGB2BGR, CV_BayerRG2BGR, CV_BayerGR2BGR, CV_BayerBG2RGB, CV_BayerGB2RGB, CV_BayerRG2RGB, CV_BayerGR2RGB ). The Bayer pattern is widely used in CCD and CMOS cameras. It enables you to get color pictures from a single plane where R,G, and B pixels (sensors of a particular component) are interleaved as follows:
The output RGB components of a pixel are interpolated from 1, 2, or 4 neighbors of the pixel having the same color. There are several modifications of the above pattern that can be achieved by shifting the pattern one pixel left and/or one pixel up. The two letters
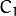 and
and
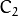 in the conversion constants CV_Bayer
in the conversion constants CV_Bayer 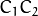 2BGR and CV_Bayer
2BGR and CV_Bayer 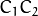 2RGB indicate the particular pattern
type. These are components from the second row, second and third
columns, respectively. For example, the above pattern has a very
popular “BG” type.
2RGB indicate the particular pattern
type. These are components from the second row, second and third
columns, respectively. For example, the above pattern has a very
popular “BG” type.
distanceTransform¶
Calculates the distance to the closest zero pixel for each pixel of the source image.
- C++: void distanceTransform(InputArray src, OutputArray dst, int distanceType, int maskSize)¶
- C++: void distanceTransform(InputArray src, OutputArray dst, OutputArray labels, int distanceType, int maskSize)¶
- Python: cv2.distanceTransform(src, distanceType, maskSize[, dst[, labels]]) → dst, labels¶
- C: void cvDistTransform(const CvArr* src, CvArr* dst, int distanceType=CV_DIST_L2, int maskSize=3, const float* mask=NULL, CvArr* labels=NULL )¶
- Python: cv.DistTransform(src, dst, distanceType=CV_DIST_L2, maskSize=3, mask=None, labels=None) → None¶
Parameters: - src – 8-bit, single-channel (binary) source image.
- dst – Output image with calculated distances. It is a 32-bit floating-point, single-channel image of the same size as src .
- distanceType – Type of distance. It can be CV_DIST_L1, CV_DIST_L2 , or CV_DIST_C .
- maskSize – Size of the distance transform mask. It can be 3, 5, or CV_DIST_MASK_PRECISE (the latter option is only supported by the first function). In case of the CV_DIST_L1 or CV_DIST_C distance type, the parameter is forced to 3 because a
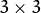 mask gives the same result as
mask gives the same result as 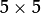 or any larger aperture.
or any larger aperture. - labels – Optional output 2D array of labels (the discrete Voronoi diagram). It has the type CV_32SC1 and the same size as src . See the details below.
The functions distanceTransform calculate the approximate or precise distance from every binary image pixel to the nearest zero pixel. For zero image pixels, the distance will obviously be zero.
When maskSize == CV_DIST_MASK_PRECISE and distanceType == CV_DIST_L2 , the function runs the algorithm described in [Felzenszwalb04].
In other cases, the algorithm
[Borgefors86]
is used. This means that
for a pixel the function finds the shortest path to the nearest zero pixel
consisting of basic shifts: horizontal,
vertical, diagonal, or knight’s move (the latest is available for a
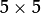 mask). The overall distance is calculated as a sum of these
basic distances. Since the distance function should be symmetric,
all of the horizontal and vertical shifts must have the same cost (denoted as a ), all the diagonal shifts must have the
same cost (denoted as b ), and all knight’s moves must have
the same cost (denoted as c ). For the CV_DIST_C and CV_DIST_L1 types, the distance is calculated precisely,
whereas for CV_DIST_L2 (Euclidian distance) the distance
can be calculated only with a relative error (a
mask). The overall distance is calculated as a sum of these
basic distances. Since the distance function should be symmetric,
all of the horizontal and vertical shifts must have the same cost (denoted as a ), all the diagonal shifts must have the
same cost (denoted as b ), and all knight’s moves must have
the same cost (denoted as c ). For the CV_DIST_C and CV_DIST_L1 types, the distance is calculated precisely,
whereas for CV_DIST_L2 (Euclidian distance) the distance
can be calculated only with a relative error (a
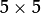 mask
gives more accurate results). For a,``b`` , and c , OpenCV uses the values suggested in the original paper:
mask
gives more accurate results). For a,``b`` , and c , OpenCV uses the values suggested in the original paper:
| CV_DIST_C | 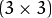 |
a = 1, b = 1 |
|---|---|---|
| CV_DIST_L1 | 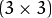 |
a = 1, b = 2 |
| CV_DIST_L2 | 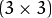 |
a=0.955, b=1.3693 |
| CV_DIST_L2 | 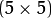 |
a=1, b=1.4, c=2.1969 |
Typically, for a fast, coarse distance estimation CV_DIST_L2, a
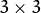 mask is used. For a more accurate distance estimation CV_DIST_L2 , a
mask is used. For a more accurate distance estimation CV_DIST_L2 , a
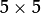 mask or the precise algorithm is used.
Note that both the precise and the approximate algorithms are linear on the number of pixels.
mask or the precise algorithm is used.
Note that both the precise and the approximate algorithms are linear on the number of pixels.
The second variant of the function does not only compute the minimum distance for each pixel
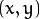 but also identifies the nearest connected
component consisting of zero pixels. Index of the component is stored in
but also identifies the nearest connected
component consisting of zero pixels. Index of the component is stored in
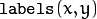 .
The connected components of zero pixels are also found and marked by the function.
.
The connected components of zero pixels are also found and marked by the function.
In this mode, the complexity is still linear. That is, the function provides a very fast way to compute the Voronoi diagram for a binary image. Currently, the second variant can use only the approximate distance transform algorithm.
floodFill¶
Fills a connected component with the given color.
- C++: int floodFill(InputOutputArray image, Point seed, Scalar newVal, Rect* rect=0, Scalar loDiff=Scalar(), Scalar upDiff=Scalar(), int flags=4 )¶
- C++: int floodFill(InputOutputArray image, InputOutputArray mask, Point seed, Scalar newVal, Rect* rect=0, Scalar loDiff=Scalar(), Scalar upDiff=Scalar(), int flags=4 )¶
- Python: cv2.floodFill(image, mask, seedPoint, newVal[, loDiff[, upDiff[, flags]]]) → retval, rect¶
- C: void cvFloodFill(CvArr* image, CvPoint seedPoint, CvScalar newVal, CvScalar loDiff=cvScalarAll(0), CvScalar upDiff=cvScalarAll(0), CvConnectedComp* comp=NULL, int flags=4, CvArr* mask=NULL )¶
- Python: cv.FloodFill(image, seedPoint, newVal, loDiff=(0, 0, 0, 0), upDiff=(0, 0, 0, 0), flags=4, mask=None) → comp¶
Parameters: - image – Input/output 1- or 3-channel, 8-bit, or floating-point image. It is modified by the function unless the FLOODFILL_MASK_ONLY flag is set in the second variant of the function. See the details below.
- mask –
(For the second function only) Operation mask that should be a single-channel 8-bit image, 2 pixels wider and 2 pixels taller. The function uses and updates the mask, so you take responsibility of initializing the mask content. Flood-filling cannot go across non-zero pixels in the mask. For example, an edge detector output can be used as a mask to stop filling at edges. It is possible to use the same mask in multiple calls to the function to make sure the filled area does not overlap.
Note
Since the mask is larger than the filled image, a pixel
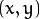 in image corresponds to the pixel
in image corresponds to the pixel 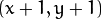 in the mask .
in the mask . - seed – Starting point.
- newVal – New value of the repainted domain pixels.
- loDiff – Maximal lower brightness/color difference between the currently observed pixel and one of its neighbors belonging to the component, or a seed pixel being added to the component.
- upDiff – Maximal upper brightness/color difference between the currently observed pixel and one of its neighbors belonging to the component, or a seed pixel being added to the component.
- rect – Optional output parameter set by the function to the minimum bounding rectangle of the repainted domain.
- flags –
Operation flags. Lower bits contain a connectivity value, 4 (default) or 8, used within the function. Connectivity determines which neighbors of a pixel are considered. Upper bits can be 0 or a combination of the following flags:
- FLOODFILL_FIXED_RANGE If set, the difference between the current pixel and seed pixel is considered. Otherwise, the difference between neighbor pixels is considered (that is, the range is floating).
- FLOODFILL_MASK_ONLY If set, the function does not change the image ( newVal is ignored), but fills the mask. The flag can be used for the second variant only.
The functions floodFill fill a connected component starting from the seed point with the specified color. The connectivity is determined by the color/brightness closeness of the neighbor pixels. The pixel at
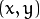 is considered to belong to the repainted domain if:
is considered to belong to the repainted domain if:
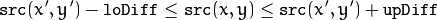
in case of a grayscale image and floating range
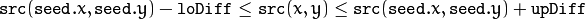
in case of a grayscale image and fixed range
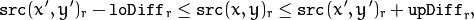
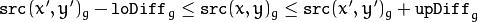
and
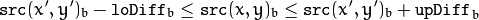
in case of a color image and floating range
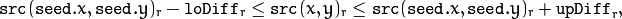
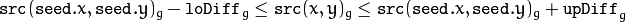
and
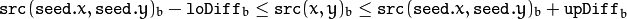
in case of a color image and fixed range
where
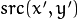 is the value of one of pixel neighbors that is already known to belong to the component. That is, to be added to the connected component, a color/brightness of the pixel should be close enough to:
is the value of one of pixel neighbors that is already known to belong to the component. That is, to be added to the connected component, a color/brightness of the pixel should be close enough to:
- Color/brightness of one of its neighbors that already belong to the connected component in case of a floating range.
- Color/brightness of the seed point in case of a fixed range.
Use these functions to either mark a connected component with the specified color in-place, or build a mask and then extract the contour, or copy the region to another image, and so on. Various modes of the function are demonstrated in the floodfill.cpp sample.
See also
findContours()
inpaint¶
Restores the selected region in an image using the region neighborhood.
- C++: void inpaint(InputArray src, InputArray inpaintMask, OutputArray dst, double inpaintRadius, int flags)¶
- Python: cv2.inpaint(src, inpaintMask, inpaintRange, flags[, dst]) → dst¶
- C: void cvInpaint(const CvArr* src, const CvArr* mask, CvArr* dst, double inpaintRadius, int flags)¶
- Python: cv.Inpaint(src, mask, dst, inpaintRadius, flags) → None¶
Parameters: - src – Input 8-bit 1-channel or 3-channel image.
- inpaintMask – Inpainting mask, 8-bit 1-channel image. Non-zero pixels indicate the area that needs to be inpainted.
- dst – Output image with the same size and type as src .
- inpaintRadius – Radius of a circlular neighborhood of each point inpainted that is considered by the algorithm.
- flags –
Inpainting method that could be one of the following:
- INPAINT_NS Navier-Stokes based method.
- INPAINT_TELEA Method by Alexandru Telea [Telea04].
The function reconstructs the selected image area from the pixel near the area boundary. The function may be used to remove dust and scratches from a scanned photo, or to remove undesirable objects from still images or video. See http://en.wikipedia.org/wiki/Inpainting for more details.
integral¶
Calculates the integral of an image.
- C++: void integral(InputArray image, OutputArray sum, int sdepth=-1 )¶
- C++: void integral(InputArray image, OutputArray sum, OutputArray sqsum, int sdepth=-1 )¶
- C++: void integral(InputArray image, OutputArray sum, OutputArray sqsum, OutputArray tilted, int sdepth=-1 )¶
- Python: cv2.integral(src[, sum[, sdepth]]) → sum¶
- Python: cv2.integral2(src[, sum[, sqsum[, sdepth]]]) → sum, sqsum¶
- Python: cv2.integral3(src[, sum[, sqsum[, tilted[, sdepth]]]]) → sum, sqsum, tilted¶
- C: void cvIntegral(const CvArr* image, CvArr* sum, CvArr* sqsum=NULL, CvArr* tiltedSum=NULL )¶
- Python: cv.Integral(image, sum, sqsum=None, tiltedSum=None) → None¶
Parameters: - image – Source image as
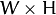 , 8-bit or floating-point (32f or 64f).
, 8-bit or floating-point (32f or 64f). - sum – Integral image as
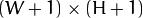 , 32-bit integer or floating-point (32f or 64f).
, 32-bit integer or floating-point (32f or 64f). - sqsum – Integral image for squared pixel values. It is
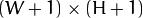 , double-precision floating-point (64f) array.
, double-precision floating-point (64f) array. - tilted – Integral for the image rotated by 45 degrees. It is
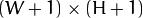 array with the same data type as sum.
array with the same data type as sum. - sdepth – Desired depth of the integral and the tilted integral images, CV_32S, CV_32F, or CV_64F.
- image – Source image as
The functions calculate one or more integral images for the source image as follows:
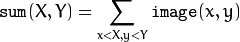
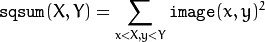
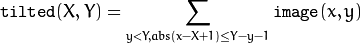
Using these integral images, you can calculate sa um, mean, and standard deviation over a specific up-right or rotated rectangular region of the image in a constant time, for example:
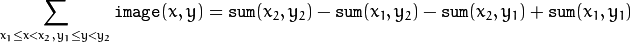
It makes possible to do a fast blurring or fast block correlation with a variable window size, for example. In case of multi-channel images, sums for each channel are accumulated independently.
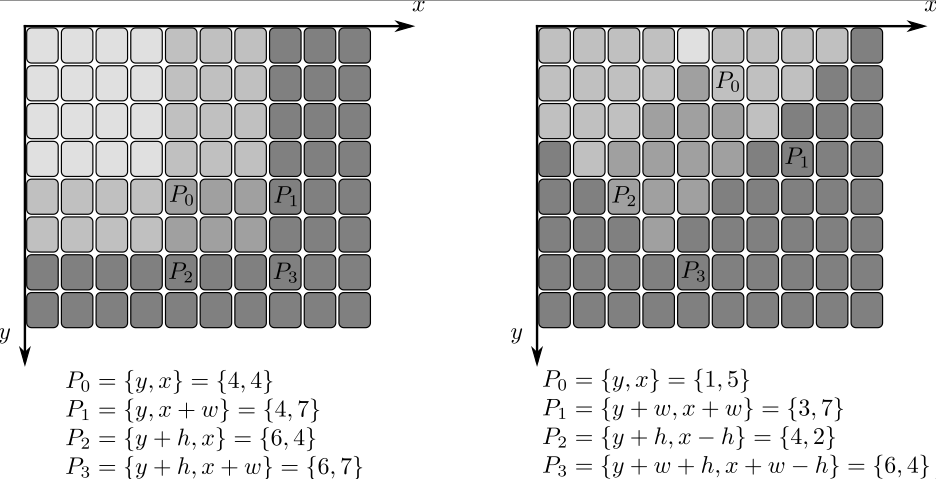
As a practical example, the next figure shows the calculation of the integral of a straight rectangle Rect(3,3,3,2) and of a tilted rectangle Rect(5,1,2,3) . The selected pixels in the original image are shown, as well as the relative pixels in the integral images sum and tilted .
threshold¶
Applies a fixed-level threshold to each array element.
- C++: double threshold(InputArray src, OutputArray dst, double thresh, double maxVal, int thresholdType)¶
- Python: cv2.threshold(src, thresh, maxval, type[, dst]) → retval, dst¶
- C: double cvThreshold(const CvArr* src, CvArr* dst, double threshold, double maxValue, int thresholdType)¶
- Python: cv.Threshold(src, dst, threshold, maxValue, thresholdType) → None¶
Parameters: - src – Source array (single-channel, 8-bit of 32-bit floating point).
- dst – Destination array of the same size and type as src .
- thresh – Threshold value.
- maxVal – Maximum value to use with the THRESH_BINARY and THRESH_BINARY_INV thresholding types.
- thresholdType – Thresholding type (see the details below).
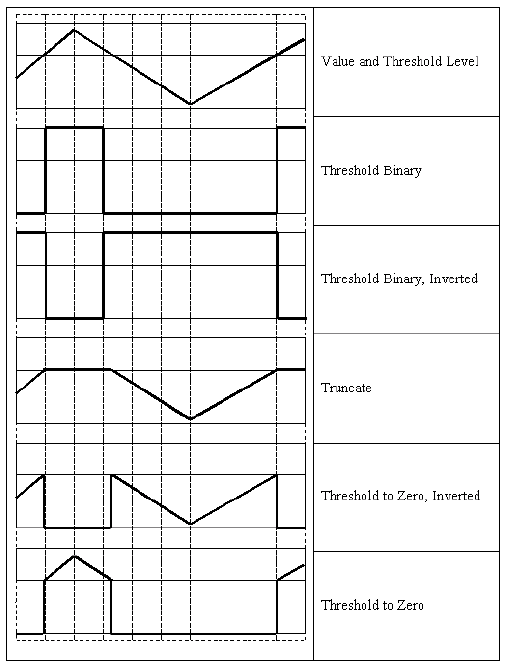
The function applies fixed-level thresholding to a single-channel array. The function is typically used to get a bi-level (binary) image out of a grayscale image ( compare() could be also used for this purpose) or for removing a noise, that is, filtering out pixels with too small or too large values. There are several types of thresholding supported by the function. They are determined by thresholdType :
THRESH_BINARY
THRESH_BINARY_INV
THRESH_TRUNC
THRESH_TOZERO
THRESH_TOZERO_INV
Also, the special value THRESH_OTSU may be combined with one of the above values. In this case, the function determines the optimal threshold value using the Otsu’s algorithm and uses it instead of the specified thresh . The function returns the computed threshold value. Currently, the Otsu’s method is implemented only for 8-bit images.
See also
adaptiveThreshold(), findContours(), compare(), min(), max()
watershed¶
Performs a marker-based image segmentation using the watershed algrorithm.
- C++: void watershed(InputArray image, InputOutputArray markers)¶
- C: void cvWatershed(const CvArr* image, CvArr* markers)¶
- Python: cv2.watershed(image, markers) → None¶
Parameters: - image – Input 8-bit 3-channel image.
- markers – Input/output 32-bit single-channel image (map) of markers. It should have the same size as image .
The function implements one of the variants of watershed, non-parametric marker-based segmentation algorithm, described in [Meyer92].
Before passing the image to the function, you have to roughly outline the desired regions in the image markers with positive (>0) indices. So, every region is represented as one or more connected components with the pixel values 1, 2, 3, and so on. Such markers can be retrieved from a binary mask using findContours() and drawContours() (see the watershed.cpp demo). The markers are “seeds” of the future image regions. All the other pixels in markers , whose relation to the outlined regions is not known and should be defined by the algorithm, should be set to 0’s. In the function output, each pixel in markers is set to a value of the “seed” components or to -1 at boundaries between the regions.
Visual demonstration and usage example of the function can be found in the OpenCV samples directory (see the watershed.cpp demo).
Note
Any two neighbor connected components are not necessarily separated by a watershed boundary (-1’s pixels); for example, they can touch each other in the initial marker image passed to the function.
See also
findContours()
grabCut¶
Runs the GrabCut algorithm.
- C++: void grabCut(InputArray image, InputOutputArray mask, Rect rect, InputOutputArray bgdModel, InputOutputArray fgdModel, int iterCount, int mode)¶
- Python: cv2.grabCut(img, mask, rect, bgdModel, fgdModel, iterCount[, mode]) → None¶
Parameters: - image – Input 8-bit 3-channel image.
- mask –
Input/output 8-bit single-channel mask. The mask is initialized by the function when mode is set to GC_INIT_WITH_RECT. Its elements may have one of following values:
- GC_BGD defines an obvious background pixels.
- GC_FGD defines an obvious foreground (object) pixel.
- GC_PR_BGD defines a possible background pixel.
- GC_PR_BGD defines a possible foreground pixel.
- rect – ROI containing a segmented object. The pixels outside of the ROI are marked as “obvious background”. The parameter is only used when mode==GC_INIT_WITH_RECT .
- bgdModel – Temporary array for the background model. Do not modify it while you are processing the same image.
- fgdModel – Temporary arrays for the foreground model. Do not modify it while you are processing the same image.
- iterCount – Number of iterations the algorithm should make before returning the result. Note that the result can be refined with further calls with mode==GC_INIT_WITH_MASK or mode==GC_EVAL .
- mode –
Operation mode that could be one of the following:
- GC_INIT_WITH_RECT The function initializes the state and the mask using the provided rectangle. After that it runs iterCount iterations of the algorithm.
- GC_INIT_WITH_MASK The function initializes the state using the provided mask. Note that GC_INIT_WITH_RECT and GC_INIT_WITH_MASK can be combined. Then, all the pixels outside of the ROI are automatically initialized with GC_BGD .
- GC_EVAL The value means that the algorithm should just resume.
The function implements the GrabCut image segmentation algorithm. See the sample grabcut.cpp to learn how to use the function.
| [Borgefors86] | Borgefors, Gunilla, Distance transformations in digital images. Comput. Vision Graph. Image Process. 34 3, pp 344–371 (1986) |
| [Felzenszwalb04] | Felzenszwalb, Pedro F. and Huttenlocher, Daniel P. Distance Transforms of Sampled Functions, TR2004-1963, TR2004-1963 (2004) |
| [Meyer92] | Meyer, F. Color Image Segmentation, ICIP92, 1992 |
| [Telea04] | Alexandru Telea, An Image Inpainting Technique Based on the Fast Marching Method. Journal of Graphics, GPU, and Game Tools 9 1, pp 23-34 (2004) |
Help and Feedback
You did not find what you were looking for?- Ask a question in the user group/mailing list.
- If you think something is missing or wrong in the documentation, please file a bug report.